聯系人:舒工
手機:13726017833
qq:64407753
地址:廣東省中山市三鄉鎮烏石村萬里路2號16卡首層
發布時間:2021-11-05 20:50:42

一、高考數學對考生的困擾。
數學對于大部分同學來說都是噩夢,深受其折磨。多數成績不理想,由數學分數的不理想從而影響成績的不在小數。多數同學拿著數學無從下手。
我們先了解一下數學這幾個問題:
1、那么難?
2、那么難考高分?
3、為什么每次考試老師解題都聽懂,后面考試又重復錯題?
4、為什么考分忽高忽低?
數學難是因為邏輯思維很強,知識點環環相扣的原因,如果少了其中的哪個環,那么數學就變難了。
數學難考高分的原因很多,主要原因還是知識點存在盲區,還有知識點應用不夠熟練。知識點關聯應用不夠熟練是什么意思呢,打個比方,我們把數學環環相扣的知識點比作項鏈上還沒有串起來的珠子,哪怕我們把珠子標上號想從其中找到我們需要的號碼也很難,就像考試,如果我們知識點不懂,考生是無法去拿知識點來解答的,因為考生不知道考什么知識點。如果我們把珠子用繩子按照順序串起來,那么找到想要的珠子就很容易找到,知識點一樣,如果我們沒有盲區知識點,對知識點梳理得比較好,遇到考題就知道要用什么知識點來解答,這也是每次考試老師解題都聽懂,后面考試又重復錯題的原因。因為老師講題的時候你知道了,但是換題目考同一個知識點你就拿他沒辦法了。
數學考試考分忽高忽低,主要原因也是存在盲區知識點,這次考試考到的題目你知識點把握不錯,你就能考到好分數,如果考到你的盲區知識點,那么丟分就是幾十分了,因為數學難題都要幾個知識點才能解答,關鍵一點難題的分值又高,有條件的考生可以去找235考試助手來梳理掃描自己的盲區知識點。

二、2022高考難易程度分析
1.低起點:體現為試卷在選擇題、填空題、解答題部分進行了系統設計,起始題起點低、入口寬,面向全體學生(如小題中的第1、2、3、4、5、6、9、10、13、14題),注重通性通法和對數學思想的考查,淡化了特殊方法、技巧解題。
2.多層次:體現為試題的難度設計上重視難度和思維的層次性(如第8、11、12、16題)。
3.高落差:體現為重視數學科高考的綜合性、創新性,在試題的難度設計上不僅有層次性,而且在思維的靈活性、深刻性,方法的綜合性、探究性和創造性等方面,科學把握試題的區分度,發揮數學科高考的選拔性功能(如第21、22題)。對學生的轉化思想、邏輯分析能力和計算能力都提出了較高的要求。為全面推進新高考政策鋪路,使其循序漸進地順利地過度下去。
三、試題變化要關注
1.“外接球問題”、“截面問題”、“導數壓軸選填題”、“導數與三角或數列相結合”等“大熱點”,本次考試未有涉及。
2.提高對知識的深度認識:選填壓軸第16題是一個以民間折紙為背景的數列題目,對學生的總結、歸納、轉化為數學模型等能力,提出了較高的要求。任何模塊的知識,都可能作為壓軸題出現在高考試題中,這也提醒我們要對高中知識掌握得夠全面、夠深度,不要忽視我們所認為的“簡單模塊”。
3.相比去年甚至往年,本次試題的數學文化、現實背景、五育并舉等背景略有減少,難度也略有降低,更多的是數學題目本身;試卷的閱讀量也略有減少,未出現結構不良試題。但8、16、18等題目還是具有社會文化背景、傳統文化背景。
四、考題變化及其分析:
考點變化1:重視數學實踐,數學建模
舉例1:為了測量兩山頂M,N間的距離,飛機沿水平方向在A,B兩點進行測量,A,B,M,N在同一個鉛垂平面內(如示意圖),飛機能夠測量的數據有俯角和A,B間的距離,請設計一個方案,包括:指出需要測量的數據(用字母表示,并在圖中標出);用文字和公式寫出計算M,N間的距離的步驟。(這些題目考試助手里都會有例舉)
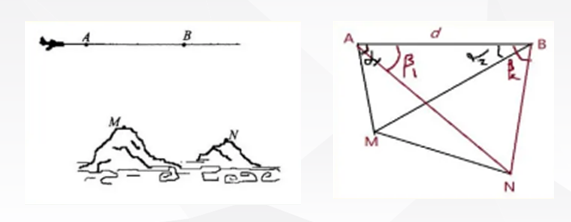
注意1:測量學是數學建模的最佳切入點。
注意2:數學新教材必修第二冊第六章《平面向量及其應用》復習參考題。

解這類題目要這樣來思考做題:讀(收集信息)想(加工信息)畫(直觀內化)
算(運算求解)寫(解決問題)五個步驟來解答。
舉例2:日晷(gui)是中國古代用來測定時間的儀器,利用與晷面垂直的晷針投射到晷面的影子來測定時間.把地球看成一個球(球心記為O),地球上一點A的緯度是指oA與地球赤道所在平面所成角,點4處的水平面是指過點4且與oA垂直的平面,在點4處放置一個日晷,若晷面與赤道所在平面平行,點4處的緯度為北緯40°,則晷針與點A處的水平面所成角為()

注意1:數學建模從嘗試到成熟(現在)歷盡艱辛,十年磨一劍中國數學發展史就是數學實踐使,為我們留下豐富的案例,也是人類的瑰寶。
舉例3:魏晉時劉徽撰寫的《海島算經》是有關測量的數學著作,其中第一題是測海島的高.如圖,點E,H,G在水平線AC上,DE和FG是兩個垂直于水平面且等高的測量標桿的高度,稱為“表高”,EG稱為“表距”,GC和EH都稱為“表目距”,GC與EH的差稱為“表目距的差”,則海島AB的高()
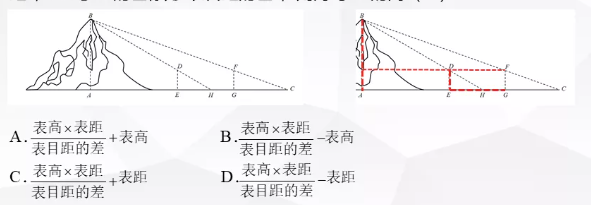
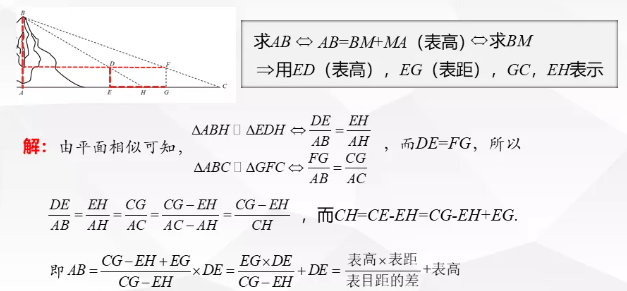
考點變化2:優化計算。
舉例1:根據有關資料,圍棋狀態空間復雜度的上限M約為3361,而可觀測宇宙中普
通物質的原子總數N約為1080則下列各數中與M/N最接近的是(參考數據: lg3≈0.48)

舉例2:青少年視力是社會普遍關注的問題,視力情況可借助視力表測量.通常用五分記錄法和小數記錄法記錄視力數據,五分記錄法的數據L和小數記錄表的數據V的滿足L=5+lgV.已知某同學視力的五分記錄法的數據為4.9,則其視力的小數記錄法的數據為(910 ~1.259 )( )
A. 1.5 B.1.2 C.0.8 D. 0.6

舉例3:古希臘時期,人們認為最美人體的頭頂至肚臍的長度與肚臍至足底的長度之比是5-1(5,-1 =0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是5-1若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26 cm,則其身高可能是.

解答思路:有的考生根據西方女性的一般身高推斷維納斯的身高在175厘米左右;有的學生涉獵較廣,自身就知道維納斯的身高;
有的根據自己的偶像明星的腿長與身高數據直接作答。
考點變化4:數學概念及基本知識深入理解
舉例1:有6個相同的球,分別標有數字1,2,3,4,5,6,從中有放回的隨機取兩次,每次取1個球.甲表示事件“第一次取出的球的數字是1”,乙表示事件“第二次取出的球的數字是2”,丙表示事件“兩次取出的球的數字之和是8”,丁表示事件“兩次取出的球的數字之和是7”,則。
A.甲與丙相互獨立
B.甲與丁相互獨立
c.之與丙相互獨立
D.丙與丁相互獨立
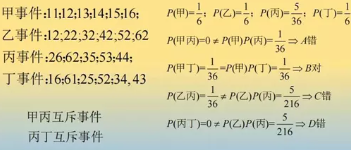
解題思路:互斥事件、對立事件,等可能事件相互獨立事件獨立重復事件。
舉例2:

考點變化5:重視一題多解,多題一解
舉例1:

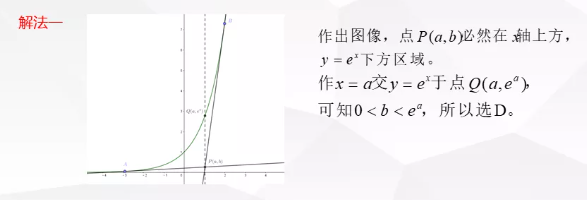


多種思路解答其實也就是數學考邏輯思維,這才能達到學習數學的目的。

掃一掃加好友